“It may be boldly asked where can the man be found, possessing the extraordinary gifts of Newton, who could suffer himself to be deluded by such a hocus-pocus, if he had not in the first instance willfully deceived himself;
Only those who know the strength of self-deception, and the extent to which it sometimes trenches on dishonesty, are in a condition to explain the conduct of Newton and of Newton’s school. To support his unnatural theory Newton heaps fiction upon fiction, seeking to dazzle where he cannot convince.
In whatever way or manner may have occurred this business, I must still say that I curse this modern history theory of Cosmology, and hope that perchance there may appear, in due time, some young scientists of genius, who will pick u courage enough to upset this universally disseminated delirium of lunatics”. ~ Johann Goethe
****
This is mostly taken from the work of Gerard Hickson in his 1922 book, “Kings Dethroned”. He lays clearly, concisely and irrefutably how astronomer by astronomer in the 16th and 17th centuries began in error by the way they measured distance from Earth to Sun, Moon and planets and then subsequently came up with preposterous theory after theory, over decades, to cover up there errors, that continues to this very day.
From Copernicus, Galileo, Kepler, Halley, Newton in Europe across the pond in the 1900’s to Einstein and NASA, astronomy has used the same errors in calculating distance of stars and planets in what is called Astrometry.
In the 1920’s, Gerrard Hickson proves conclusively, using their own geometry, math and theories of heliocentrism, gravity, relativity, etc., are gravely in gross error.
In no uncertain terms this work blows apart the Sun centered, Earth a sphere rotating, gravity based heliocentric theory that has been taught in every classroom on our flat plane Earth for the past century or more.
Enjoy!
Part II; Einstein and the Still Earth

(Original book title)
Click to access kingsdethronedhi00hickrich.pdf
****
PREFACE
In the year 1907 the author made a remarkable discovery which convinced him that the sun was very much nearer to the earth than was generally supposed.
The fact he had discovered was demonstrated beyond all doubt, so that he was compelled to believe that— however improbable it might seem— astronomers had made a mistake when they estimated the distance of the sun to be ninety-three millions of miles.
He then proceeded to examine the means by which the sun’s distance had been computed, and found an astounding error in the “ Diurnal Method of Measurement by Parallax,” which had been invented by Dr. Hailey in the early part of the 19th century, and which was used by Sir David Gill in measuring the distance to the planet Mars in 1877 ; from which he deduced his solar parallax of 8.80″.
Seeing that Sir Norman Lockyer had said that the distance to and the dimensions of everything in the firmament except the moon depends upon Sir David Gill’s measurement to Mars, the author set himself the tremendous task of proving the error, tracing its consequences up to the present day, and also tracing it backwards to the source from which it sprang.
The result of that research is a most illuminating history of the evolution of astronomy from the time of the Roman Empire up to April 1922 ; which is now placed in the hands of the people in “ Kings Dethroned.”
The author has taken the unusual course of submitting these new and startling theories for the consideration of the general public because the responsible scientific societies in London, Washington and Paris, failed to deal with the detailed accounts of the work which he forwarded to them in the Spring of 1920.
******
“How do i do it?” he said to The New York Times correspondent. ” I know where the winds come from, and no so-called meteorologist knows that. It is quite simple. The sun heats the earth more rapidly than the sea; currents of air are set up, and if you study the coast lines and hills you soon find out all about the winds.”
“But how can rays from the sun, 93,000,000 million miles away, distinguish between sea and land?” G.H., Founder of the Hicksonian Society.
WHEN THE WORLD WAS YOUNG
THREE thousand years ago men believed the earth was supported on gigantic pillars. The
sun rose in the east every morning, passed overhead, and sank in the west every evening ; then
it was supposed to pass between the pillars under the earth during the night, to re-appear in the east again next morning.
This idea of the universe was upset by Pythagoras some five hundred years before the birth of Christ, when he began to teach that the earth was round like a ball, with the sun going round it daily from east to w e s t; and this theory was already about four hundred years old when Hipparchus, the great Greek scientist, took it up and developed it in the second century, b .c . Hipparchus may be ranked among the score or so of the greatest scientists who have ever lived.
He was the inventor of the system of measuring the distance to far off objects by triangulation, or trigonometry, which is used by our surveyors at the present day, and which is the basis of all the methods of measuring distance which are used in modern astronomy. Using this method of his own invention, he measured from point to point on the surface of the earth, and so laid the foundation of our present systems of geography, scientific map-making and navigation.
No star is more than 10,000 miles away, and the sun never more than 7,500. How did he prove that? Why, by triangulation, of course. The astronomers used the system suggested by Halley, but it was ridiculous. Mr. Hickson just made New York one end, and calculated from that. Had he been to his southern observation point? No, but he had made a model and worked it out from that.

A triangle must add up to 180 degrees. When laid out flat it is one-half of a circle of 360 degrees. By having two points known, a third can be determined.
Triangulation.
The principles of triangulation are very simple, but because it will be necessary— as I proceed— to show how modern astronomers have departed from them, I will explain them in detail. Every figure made up of three connected lines — or three-angle, quite regardless of the length of any of its sides.
The triangle differs from all other shapes or figures in this ;— that the value of its three angles, when added together, admits of absolutely no variation ; they always equal i8o degrees ; while — on the other hand— all other figures contain angles of 360 degrees or more.
The triangle alone contains 180 degrees, and no other figure can be used for measuring distance. There is no alternative whatever, and therein lies its value. It follows, then, that if we know the value of any two of the angles in a triangle we can readily find the value of the third, by simply adding together the two known angles and subtracting the result from 180. The value of the third angle is necessarily the remainder.
“Now you have got it, ” replied Mr. Hickson. “Who told you the sun was 93,000,000 miles away? Why, the astronomers. And who told the astronomers? Why, other astronomers. You can carry it back to Copernicus-yes, to Hipparchus. They all repeat what others have said. They are all in a conspiracy.”
And now it is for us to very carefully study this fundamental idea of the Heliocentric theory, for there is an error in it.
Ptolemy had made it appear that the sun and stars revolved around a stationary earth, but Copernicus advanced the theory that it was the earth which revolved around a stationary sun, while the stars were fixed ; and either of these entirely opposite theories gives an equally satisfactory explanation of the appearance of the sun by day and the stars by night.
Copernicus did not produce any newly discovered fact to prove that Ptolemy was wrong, neither did he offer any proof that he himself was right, but worked out his system to show that he could account for all the appearances of the heavens quite as well as the Egyptian had done, though working
on an entirely different hypothesis ; and offered his new Heliocentric Theory as an alternative.
He argued that it was more reasonable to conceive the earth to be revolving round the sun than it was to think of the sun revolving round the earth, because it was more reasonable that the smaller body should move round the greater.
We see that Copernicus recognised the physical law that the lesser shall be governed by the greater, and that is the pivot upon which the whole of his astronomy turns ; but it is perfectly clear that in building up his theories he assumed the earth to be much smaller than the sun, and also smaller than the stars ; and that was pure assumption unsupported by any kind of fact.
In the absence of any proof as to whether the earth or the sun was the greater of the two, and having only the evidence of the senses to guide him, it would have been more reasonable had he left astronomy as it was, seeing that the sun appeared to move round the earth, while he himself was unconscious of any movement.
When he supposed the stars to be motionless in space, far outside the solar system, he was assuming them to be infinitely distant; relying entirely upon.
The statement made by Hipparchus seventeen hundred years before. It is strange that he should have accepted this single statement on faith while he was in the very act of repudiating all the rest of the astronomy of Hipparchus and Ptolemy, but the fact remains that he did accept the ” infinitely distant ” doctrine without question, and that led him to suppose the heavenly bodies to be proportionately large; hence the rest of his reasonings followed as a matter
of course.
He saw that the Geocentric Theory of the universe did not harmonise with the idea that the stars were infinitely distant, and so far we agree with him. He had at that time the choice of two courses open to him:—he might have studied the conclusion which had been arrived at by Hipparchus, and found the error there ; but instead of doing that he chose to find fault with the whole theory of the universe, to overthrow it, and invent an entirely new astronomy
to fit the error of Hipparchus !
It was a most unfortunate choice, but it is now made clear that the whole work of Copernicus depends upon the single question whether the ancient Greek was right or wrong when he said “ the heavenly bodies are infinitely distant.”
It is a very insecure foundation for the whole of Copernican or modern astronomy to rest upon, but such indeed is the case.

Immediately following him came Johann Kepler, and it is a very remarkable circumstance that this German philosopher, mystic and astrologer, should have been the founder of what is now known as Physical Astronomy.
Believer as he was in the ancient doctrine that men’s lives are pre-destined and mysteriously influenced by the stars and planets, he nevertheless sought to discover some physical law
which governed the heavenly bodies.
Having accepted the Copernican Theory that the sun was the centre of the universe, and that the earth and the planets revolved around it, it was but natural that all his reasonings and deductions should conform to those ideas, and so it is only to be expected that his conclusions dealing with the relative distances, movements and masses of the planets, which he laboured upon for many years, and which are now the famous “ Laws of Kepler,” should be in perfect accord with the Heliocentric Theory of Copernicus.
But, though the underlying principles of Kepler’s work will always have great value, his conclusions cannot be held to justify Copernican astronomy, since they are a sequel to it, but— on the contrary—they will be involved in the downfall of the theory that gave them birth.
While the life work of Johann Kepler was drawing to a close, that of Galileo was just beginning, and his name is more widely known in connection with modern astronomy than is that of its real inventor, Nicholas Copernicus.
Galileo adopted the Copernican theory with enthusiasm, and propagated it so vigorously
that at one time he was in great danger of being burnt at the stake for heresy. In the year 1642 he invented the telescope, and so may be said to have founded the modern method of observing the heavens.
Zealous follower of Copernicus as he was, Galileo did much to make his theory widely known and commonly believed, and we may be sure that it was because he saw no error in it that other giants of astronomy who came after him accepted it the more readily.
Nearly eighteen hundred years had passed since Hipparchus had said the heavenly bodies were
infinitely distant, and still no one had questioned the accuracy of that statement, nor made any attempt whatever to measure their distance.
It is interesting to mention here an event which— at first sight— might seem inimportant, but which—now reviewed in its proper place in history— can be seen to have had a marked effect on the progress of astronomy as well as navigation. This was the publication of a little book called ” The Seaman’s Practice,” by Richard Norwood, in the year 1637.
At that time books of any kind were rare, and this was the first book ever written on the subject of measuring by triangulation. It was intended for the use of mariners, but there is no doubt that ‘ ‘ The Seaman’s Practice ” helped King Charles II. to realize how the science of astronomy could be made to render valuable service to British seamen in their voyages of discovery, with the result that in 1675 he appointed John Flamsteed to make a special study of the stars, and to chart them after the manner of Tycho Brahe and Galileo, in order that navigators might guide their ships by the constellations over the trackless oceans.
That was how the British School of Astronomy came into existence, with John Flamsteed as the first Astronomer Royal, employing only one assistant, with whom he shared a magnificent salary of £70 a year ; and navigation owes much to the excellent work he did with an old-fashioned telescope, mounted in a little wooden shed on Greenwich Hill.
At about the same time the French School of Astronomy came into being, and the end of the
seventeenth century began the most glorious period in the history of the science, when astronomers in England, France and Germany all contested strenuously for supremacy, and worshiped at the shrine of Copernicus.

GIANTS OF MODERN ASTRONOMY
Before passing on to the more important part of this work, it is only just to record the fact that the first practical work in triangulation since the time of Hipparchus was performed by Jean Picard and J. and D. Cassini, between Paris and Dunkirk toward the end of the 17th century ; when Newton was working out his theories.
At this time the Copernican theory of astronomy was well established, and was accepted by all the scientific world, though it is probable that the public in general found it difficult to reconcile the idea of an earth careering through space at prodigious speed with common sense and reason. Even the most ardent followers of Copernicus and Galileo recognised this difficulty, and some strove to find a satisfactory explanation.
Nearly a hundred years ago Kepler had suggested that some kind of unknown force must hold the earth and the heavenly bodies in their places, and now Sir Isaac Newton, the greatest mathematician of his age, took up the idea and built the Law of Gravitation.
The name is derived from the Latin word “ gravis,” which means “ heavy,” “ having weight,” while the Law of Gravitation is defined as “ That mutual action between masses of matter by virtue of which every such mass tends toward every other with a force varying directly as the product of the masses, and inversely as the square of their distances apart.”
Reduced to simplicity, gravitation is said to be “ That which attracts every thing toward every other thing.” That does not tell us much ; and yet the little it does tell us is not true ; for a thoughtful observer knows very well that everything is not attracted towards every other thing. . . The definition implies that it is a force ; but it does not say so, for that phrase “ mutual action ” is ambiguous, and not at all convincing.
The Encyclopaedia Britannica tells us that “ The Law of Gravitation is unique among the laws of nature, not only for its wide generality, taking the whole universe into its scope, but in the fact that, so far as is yet known, it is absolutely unmodified by any condition or cause whatever.”
Here again we observe that the nature of gravitation is not really defined at all ; we are told that masses of matter tend toward each other, but no reason is given why they do so, or should do so ; while to say that “ it is absolutely unmodified by any condition or cause whatever ” is one of the most unscientific statements it is possible to make.
There is not anything or force in the universe that is absolute! No thing that goes its own way and does what it will without regard to other forces or things. The thing is impossible; and it is not true; wherefore it has fallen to me to show where the inconsistency in it lies.
The name given to this mutual action means “ weight,” and weight is one of the attributes of all matter. Merely to say that anything is matter or material implies that it has weight, while to speak of weight implies matter. Matter and weight are inseparable, they are not laws, but elemental facts. They exist.
But it has been suggested that gravitation is a force, indeed we often hear it referred to as the force of gravitation ; but force is quite a different thing than weight, it is active energy expressed by certain conditions and combinations of matter. It acts.
All experience and observation goes to prove that material things fall to earth because they possess the attribute of weight, and that an object remains suspended in air or space only so long as its weight is overcome by a force, which is contrary. And when we realize these simple facts we see that gravitation is in reality conditioned and modified by every other active force, both great and small.
Again, gravitation is spoken of as a pull, an agent of attraction that robs weight of its meaning, something that brings all terrestrial things down to earth while at the same time it keeps the heavenly bodies in their places and prevents them falling toward each other or apart. The thing is altogether too wonderful, it is not natural; and the theory is scientifically unsound. . .
Every man, however great his genius, must be limited by the conditions that surround him ; and
science in general was not sufficiently advanced two hundred years ago to be much help to Newton, so that— for lack of information which is ordinary knowledge to us having in the 20th century— he fell into the error of attributing the effects of “ weight ” and “ force ” to a common cause, which— for want of a better term— he called gravitation ; but I have not the slightest doubt that if he were living now he would have arrived at the following more reasonable conclusions:— That terrestrial things fall to earth by “ gravis,” weight; because they are matter ; while the heavenly bodies (which also are matter) do not fall because they are maintained in their courses by magnetic or electric force.

Another figure of great prominence in the early part of the eighteenth century was Dr. Hailey, who survived Sir Isaac Newton by some fifteen years, and it is to him that we owe nearly all the methods of measuring distance which are used in astronomy at the present day. So far no one had seriously considered the possibility of measuring the distance to the sun planets or stars since Hipparchus had failed— away back in the second century B.C.— but now, since the science had made great strides, it occurred to Dr. Hailey that it might be possible at least to find the distance from the earth to the sun, or to the nearest planet.
Measuring Stars At A Distance
Remembering the time-honoured dogma that the stars are infinitely distant, inspired by the magnificence of the Copernican conception of the universe, and influenced— no doubt— by the colossal suggestions of Ole Roemer, he tried to invent some means of making a triangulation on a gigantic scale, with a base-line of hitherto unknown dimensions.
Long years ago Kepler had worked out a theory of the distances of the planets with relation to each other, the principle of which— when expressed in simple language and in round figures— is as follows :
“ If we knew the distance to any one of the planets we could use that measurement as a basis from which to estimate the others. Thus Venus is apparently about twice as far from the sun as Mercury, while the earth is about three times and Mars four times as far from the sun as Mercury, so that should the distance of the smallest planet be— let us say— 50 million miles, then Venus would be 100, the Earth 150, and Mars 200 millions of miles.”
This seems to be the simplest kind of arithmetic, but the whole of the theory of relative distance goes to pieces because Kepler had not the slightest idea of the linear distance from the earth to anything in the firmament, and based all his calculations on time, and on the apparent movements of the planets in azimuth, that is— to right or left of the observer, and to the right or left of the sun.
Necessity compels me to state these facts in this plain and almost brutal fashion, but it is my sincere hope that no reader will suppose that I under-estimate the genius or the worth of such men as Newton and Kepler ; for it is probable that I appreciate and honour them more than do most of those who blindly worship them with less understanding. I only regret that they were too ready to accept Copernican astronomy as though it were an axiom, and did not put it to the proof ; and that, as a consequence, their fine intelligence and industry should have been devoted to the glorification of a blunder.
Kepler’s work was of that high order which only one man in a million could do, but nevertheless, his calculations of the relative distances of the planets depends entirely upon the question whether they revolve round the sun or not ; and that we shall discover in due course.
However, Dr. Hailey had these theories in mind when he proposed to measure the distance to Mars at a time when the planet reached its nearest point to earth (in opposition to the sun), and then to multiply that distance by three (approximate), and in that manner estimate the distance of the sun.

He proceeded then to invent what is now known as the “ Diurnal Method of Measurement by Parallax,” which he described in detail in the form of a lecture to contemporary astronomers, introducing it by remarking that he would probably not be living when next Mars came into the required position, but others might at that time put the method into practice.
He began by saying that “ If it were possible to place two observers at points diametrically opposite to each other on the surface of the earth (as A and Bin dia^am 5), both observers— looking along their respective horizons— would see Mars at the same time,the planet being between them, to the east of one observer and to the westward of the other.
In these circumstances the diameter of the earth might be used as a base-line, the observers at A and B might take simultaneous observations, and the two angles obtained, on being referred to the base-line, would give the distance of the planet.
But this was in the reign of George II. long before the invention of steamships, cables or telegraphs, and Dr. Hailey knew that it was practically impossible to have B taking observations in the middle of the Pacific Ocean, so he proposed to overcome the difficulty by the following expedient:— He suggested that both the observations could be taken by a single observer, using the same observatory, thus—
“ Let an observer at A take the first observation in the evening, when Mars will be to his east : let him then wait twelve hours, during which time the rotation of the earth will have carried him round to B. He may then take his second observation. Mars being at this time to his west, and the two angles thus obtained— on being referred to the base-line— will give the distance of the planet.”
This proposition is so plausible that it has apparently deceived every astronomer from that day to this, and it might even now deceive the reader himself were it not that he knows I have some good reason for describing it here.
It is marvelously specious ; it does not seem to call for our examination ; and yet it is all wrong! and Dr. Hailey has a world of facts against him. He is at fault in his premises, for if the planet was visible to one of the observers it must be above his horizon, and, therefore, could not be seen at the same time by the other ; since it could not be above his horizon also at both A and B points on Earth.
Again, his premises are in conflict with Euclid, because he supposes Mars to be midway between A and B, that is between their two horizons, which are parallel lines 8,000 miles apart throughout their entire length, and so it is obvious that if the planet— much smaller than the earth— was really in that position it could not be seen by either of the observers.
The alternative which Dr. Hailey proposes is as fallacious as his premises, for he overlooks the fact that— according to Copernican astronomy— during the twelve hours while the earth has been rotating on its axis it has also travelled an immense distance in its orbit round the sun.
THE DISTANCE TO THE MOON
Let us pass on to something more important, the measurement of the distance to the moon, the first of the heavenly bodies to be measured. This was performed by Lalande and Lacaille in the year 1752, using the method of direct triangulation. Lalande took one of the observations at Berlin, while Lacaille took the other at the same time at the Cape of Good Hope ; a straight line (or chord) joining these two places giving them a base-line more than 5,000 miles in length.
The moon was at a low altitude away in the west, the two observers took the angles with extreme care, and at a later date they met, compared notes, and made the necessary calculations. As a result the moon was said to be 238,830 miles from the earth, and to be 2,159.8 miles in diameter, the size being estimated from its distance; and these are the figures accepted in astronomy the world over at the present day.
I have occasion to call the reader’s attention to the fact that some books— Proctor’s “ Old and New Astronomy ” for example— in describing the principle of how to measure to the moon, illustrate it by a diagram which differs from the diagram above.
Though the principle as it is explained in those books seems plausible enough, it would be impossible in practice, for the diagram they use clearly shows the moon to be near the zenith. Further, it is often said that the distance to the moon has been several times measured, but the fact is that it is of no consequence whether it has or not, for it is the result obtained by Lalande and Lacaille which is accepted by astronomy, and their observations were taken as I have stated.
Moreover, one of the greatest living authorities on astronomy tells us that their work was done with such precision that “ the distance of the moon is positively settled, and is known with greater accuracy than is the length of any street in Paris.” Nevertheless we will submit it to the test.
There is every reason to believe that the practical work of these two Frenchmen was most admirably done, and yet their labours were reduced to naught, and the whole object of the triangulation was defeated, because, in making the final computations they made ” allowances ” in order to conform to certain of the established false theories of astronomy.

The “What you see is not what is Theory”
One of these is the Theory of Atmospheric Refraction, which would have us believe that when we see the sun (or moon) low down on the horizon, at sunrise or sunset, it is not really the sun itself that we see, but only an image or mirage of the sun reflected up to the horizon by atmospheric refraction, the real sun being at the time at the extremity of a line drawn through the centre of the earth, 4,000 miles below our horizon. (That is according to the astronomy taught in all schools.)
According to this theory there is at nearly all times some degree of refraction, which varies with the altitude of the body under observation, so that (in simple) the theory declares that the real moon was considerably lower than the moon which Lalande and Lacaille actually saw, for that was only a refracted image.
They had therefore, to make an allowance for atmospheric refraction. They had to find (by theory) where the real moon would be, and then they had to modify the angles they had obtained in practical triangulation, by making an allowance for what is known as “ Equatorial Parallax.”
Equatorial Parallax is defined a:
“ the apparent change in the direction of a body when seen from the surface of the earth as compared with the direction it would appear to be in if seen from the centre of the earth.”
It is difficult not to laugh at theories such as these, but I can assure the reader that astronomers take them quite seriously.
If we interpret this rightly, it is suggested that if Lalande and Lacaille will imagine themselves to be located in the centre of the earth they will perceive the moon to be at a lower altitude than it appeared to them when they saw it from the outside of the earth; and modern Copernican astronomy required that on their return to Paris they should make allowance for this.
Now observe the result. It has been shown that “Equatorial Parallax” is only altitude ; it is a question of higher or lower; it has to do with observations taken from the top of the earth compared with others taken theoretically from the centre.
Really it is an imaginary triangulation, where the line E P in diagram 9 becomes a base-line.
The line E P is vertical; therefore it follows that the theoretical triangulation by which Equatorial
Parallax is found is in the vertical plane. . . We remember, however, that the moon was away in the west when seen by Lalande and Lacaille, while their base-line was the chord (a straight line running north and south) connecting Berlin with the Cape of Good Hope.
By that almost inconceivable blunder real and imaginary angles came into conflict on two different planes, so the triangulation was entirely lost ; and as a consequence the distance of the moon is no more known to-day than it was at the time of the flood. All other attempts to measure the distance to the moon since that time have been defeated in a similar manner.
ROMANTIC THEORIES

An atom is “ the smallest conceivable particle of matter,” that is— smaller than the eye can see, even
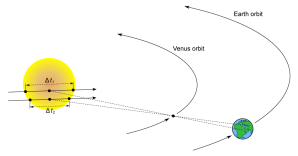
The method of finding the distance to the sun, at such a time, is as follows:— Two observers are to be placed as far apart as possible on the earth. Make B and S two positions from Earth. From these positions we will see Venus cross the face of the sun the parallel lines on the Sun, while we will see the
An “angle of parallax ” is the angle at the star, or at the apex of an astronomer’s triangulation. The angle of parallax 0.31″ (thirty-one hundredths of a second of arc) is so extremely small that it represents only one 11,613th part of a degree.
*
There is in Greenwich Observatory an instrument which lies a vernier six feet in diameter, one of the largest in the world. A degree on this vernier measures about three-quarters of an inch, so that if we tried to measure the parallax 0.31 on that vernier we should find it to be one 15,484th part of an inch.
*


The “Theory of Parallax ” as stated in astronomy, is “that the nearer the star the greater the parallax ; hence the greater the apparent displacement the nearer the body or star must be.”
The “Theory of Perpendicularity” tells us that all stars are perpendicular tothe centre of the earth, no matter what direction they may appear to be in aswe see them from different points on the surface; and proves it by “Geocentric Parallax.”


The two meridians and lines of sight are parallel, so that if continued for ever they can never meet at a point, and the two angles at the base equal 180 degrees, yet the stars are on both lines. It is obvious, therefore, that the stars have moved to the left (east), precisely as much as the earth has

Tablet VAT 4956 is an astronomical diary that records 13 lunar observations, and 15 planetary. It details the position of the moon and the planets in regard of certain stars and constellations, indicating the days and the months throughout the year 37 of the reign of Nebuchadnezzar, the king of Babylon; and the astronomical observations recorded in this tablet, can only correspond to the year 567 BC.
The fact of isolating a single observation in order to attribute the tablet to some other year would be naive and useless; the astronomers point out that an identical combination of astronomical positions repeats only every 40,000 years, so the observations recorded could only coincide with the astronomical sky of tens thousands of years before.
The lunar eclipse in the 15th day of the third month, described on 14th line of the obverse side of the tablet, took place, according to modern calculations, in July 4th of 567 BC; this eclipse started in the evening and could not be seen from Babylon. The Babylonian astronomer computed it on the base of the eclipse cycle called Saros1), and then wrote “atalû Sin”, or “calculated lunar eclipse”, and “Sa Lu”, or “unseen because of the weather”, perhaps because the sky was cloudy. (Source)
” the moon rose at 5.29, the sun set at 5.39, and the total eclipse of the moon began before the sun had set.”
“ This is an appearance merely due to refraction. The sun, already below the horizon, is raised by refraction, and remains visible to us. It is the same with the moon, which has not yet really risen when it seems to have already done so.”
“ One of the noblest achievements in Astronomy, upon which depends the distance to and the dimensions of everything in the firmament except the moon.”
Distance to Mars, 35,000,000X2.6571 = 93,000,000miles.

say— it was supposed to be only an optical or apparent displacement due to the change in the position of the observer from A to B, hence a world of romance is built upon that httle angle in this fashion : Angle of Mars 23″ = 35,000,000 miles, .-.35,000,000×2.6571 =93,000,000= solar parallax 8.80’ = distance of the sun .-.the sun’s diameter is 875,000 miles; weight XYZ lbs., age 17,000,000 years, and will probably be burnt out in another 17 million years.*
” So Mr. Hickson has his own view of the universe – a stationary earth with stars rotating around it – and when the astronomers deign to answer him publicly he will confute them utterly.*Then will his weather forecasts receive the respect that is their due and he will confer blessings on mankind and gain profit himself.*Meanwhile the police have stopped his street lectures, and he can do nothing but hang out his challenge until some one takes it up.” LONDON, special to NY Times, March 4, 1921
Since then no books on a geocentric, a flat earth round Earth has been published until Eric Dubay published the “Flat Earth Conspiracy” in 2014. I highly encourage everyone to get this most important book to understand, and help end, 500 years of one massive Lie.
It is also important to understand how the Greatest Lie in 500 years was initiated by the Vatican when books first began to be published to the Commoner and has been perpetuated by the Royal Society of Astronomer’s in London, to Einstein, to NASA. This will be covered in a subsequent post.
Please also review the “Very Brief Heliocentric History Timeline”
And Sir Isaac Newton’s 500 year Lie
#25 Is Sir Isaac Newton’s “Law of Gravity” Just One Great Big 500 Yr. Old Lie?
This is a new Age of Discovery to go within and understand the history, the mechanics, and the massive hoax that has been ongoing, yet ending now, for over 20 generations.
Part II, TBA
Tagged: astrometry, astronomy, copernicus, galileo, gerrard hickson, hicksonian society, newton




∇ Replace His-story With True-story ∇
My sense is, this is the era for truth seekers to freely share the facts over the internet for the collective consciousness to increase awareness and manifest a intentional joyful experience replacing the Age of Deception.
My intention is to experience freedom as individual sovereignty and remove the deceptive mystery of this construct, aka earthly realm.
The details about the Arc-tic circle and the Antarc-tic circle needs to be shared, as does the altitude extreme and the extreme depth below sea level…
Interesting to note John Kerry’s recent public agenda claims another treaty restricts Antarc-tic, which merely increases my curiosity for that region.
But rather than confront armed security enforcing globalist’s institutional policy, I am thinking about deploying relatively cheap miniature drones to video record the regions for the worldwide internet to see.
Remember, you are not alone and the truth will not remain hidden.
LikeLiked by 1 person